一、涡旋光和轨道角动量

         由静电的麦克斯韦方程组可知光是一种电磁波，具有能量和动量。动量可以分为线动量和角动量，角动量包括由偏振性决定的自旋角动量（Spin Angular Momentum，SAM）和由光场空间分布决定的轨道角动量（Orbital Angular Momentum，OAM）。

 

        当激光光束具有螺旋形的波前结构时，就称它为涡旋光。由于螺旋形波前位相信息不确定性引起的强度相干相消，涡旋光束中心处的相位无法确定，因此中心处存在一个位相奇点，使其界面光强呈环状分布。

    

    涡旋光束中的光子具有方位角相关的位相项exp(ilφ)，其中l为角量子数，也称为拓扑电荷数,理论上可以取任意整数；φ为空间方位角。涡旋光束中每个光子携带了lℏ（约化普朗克常量）的轨道角动量（OAM）。

                     

 

                                ▲ 高斯光束与涡旋光束相位面 

        （a）基模高斯光束的平面波前；（b）l=1轨道角动量光束的等相位面；（c）l=2具有二重螺旋的等相位面；（d）l=3具有三重螺旋的等相位面；（e）形象地说明l=3的三重螺旋相位具有类似意大利面的造型。

 

二、轨道角动量的应用

      光子轨道角动量已经成为光学领域的一个研究热点，在基础物理、应用物理以及天文、生物等交叉学科中的研究中都具有重要的应用价值。

1、由于轨道角动量光束具有特殊的螺旋相位和中空光场，因此可应用于微观世界的微操控技术。例如光学镊子，光学扳手，光学引导，微马达。

2、由于光子轨道角动量本征态在数学上构成了一组完备的正交基矢，因此可以利用轨道角动量来实现高维度信息的编码，这种信息不仅体现在经典光通信领域，也体现在量子通信领域。量子通信领域中，轨道角动量可构成无穷维的Hibert空间，可显著提高信息的容量和安全性。

 

三、高阶轨道角动量的产生

        用于产生轨道角动量光束的设备，主要包括叉形衍射光栅，螺旋位相板，柱透镜组合，集成轨道角动量发射器等。其中，叉形光栅，可以使用空间光调制器计算全息产生。空间光调制器是一种像素化的液晶显示器，每个像素都能独立调控反射光波的相位，通过软件控制，实时而便捷的产生各种图样的计算机全息光栅，具有高刷新速率、针对多种不同波长、高精度、高灵活性等特点，因而成为产生轨道角动量光束最常用的设备。

 

        通过在空间光调制器软件上加载不同的相位图，可以获得不同阶次的涡旋光束。空间光调制器的调制精度，会影响产生涡旋光的光斑质量，因此针对涡旋光的应用，选择空间光调制器要优先考虑和精度相关的参数，例如线性度、相位稳定性、衍射效率、表面平整度等。

                              

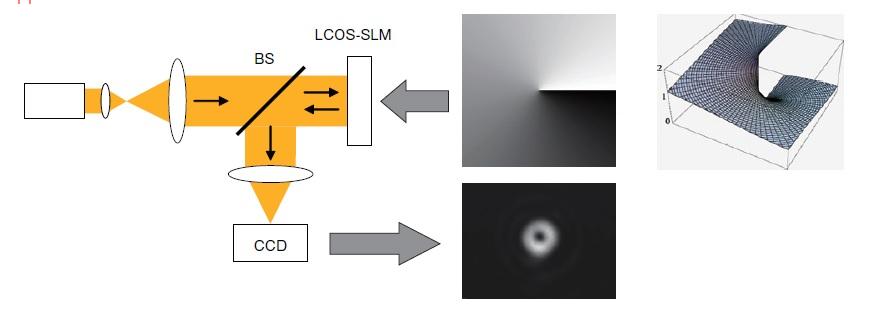
                                  ▲ 产生涡旋光束的光路示意图

 

                         

                                  ▲加载相位图与对应产生的涡旋光束

 

四、空间光调制器及相机产品

空间光调制器用于轨道角动量应用，具有以下优势：

●  光利用率高

●  一级衍射效率高

●  线性度高

●  相位稳定性高

●  表面平整度高

●  损伤阈值高

 

                                         ▲ 空间光调制器产品

 

       在实验中，一般还需要用相机去观察产生的复杂和高阶的涡旋光斑，并对其做一系列的分析。我们还可提供科研级相机，用于涡旋光的观察。InGaAs相机，光谱响应范围900-1700nm，覆盖光通信用的1550nm波长，具有制冷、高灵敏度、高分辨率、低坏点率、实时图像校正、高帧速、模拟数字同时输出等特点。可见光CMOS相机，具有高分辨率、高灵敏度、高帧速、高动态范围等优点。

                                                                      

                                      ▲ InGaAs相机                                                                           ▲ 可见光CMOS相机